PyBroom Example - Multiple Datasets - Scipy Robust Fit

This notebook is part of pybroom.

This notebook demonstrate using pybroom when fitting a set of curves (curve fitting) using robust fitting and scipy. We will show that pybroom greatly simplifies comparing, filtering and plotting fit results from multiple datasets. See pybroom-example-multi-datasets for an example using lmfit.Model instead of directly scipy.

In [1]:

%matplotlib inline
%config InlineBackend.figure_format='retina'  # for hi-dpi displays
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import normpdf
import seaborn as sns
from lmfit import Model
import lmfit
print('lmfit: %s' % lmfit.__version__)

lmfit: 0.9.5

/home/docs/checkouts/readthedocs.org/user_builds/pybroom/envs/stable/lib/python3.4/site-packages/IPython/html.py:14: ShimWarning: The `IPython.html` package has been deprecated. You should import from `notebook` instead. `IPython.html.widgets` has moved to `ipywidgets`.
  "`IPython.html.widgets` has moved to `ipywidgets`.", ShimWarning)

In [2]:

sns.set_style('whitegrid')

In [3]:

import pybroom as br

Create Noisy Data

We start simulating N datasets which are identical except for the additive noise.

In [4]:

N = 200

In [5]:

x = np.linspace(-10, 10, 101)

In [6]:

peak1 = lmfit.models.GaussianModel(prefix='p1_')
peak2 = lmfit.models.GaussianModel(prefix='p2_')
model = peak1 + peak2

In [7]:

#params = model.make_params(p1_amplitude=1.5, p2_amplitude=1,
#                           p1_sigma=1, p2_sigma=1)

In [8]:

Y_data = np.zeros((N, x.size))
Y_data.shape, x.shape

Out[8]:

((200, 101), (101,))

In [9]:

for i in range(Y_data.shape[0]):
    Y_data[i] = model.eval(x=x, p1_center=-1, p2_center=2,
                           p1_sigma=0.5, p2_sigma=1,
                           p1_height=1, p2_height=0.5)
Y_data += np.random.randn(*Y_data.shape)/10

Add some outliers:

In [10]:

num_outliers = int(Y_data.size * 0.05)
idx_ol = np.random.randint(low=0, high=Y_data.size, size=num_outliers)
Y_data.reshape(-1)[idx_ol] = (np.random.rand(num_outliers) - 0.5)*4

In [11]:

plt.plot(x, Y_data.T, 'ok', alpha=0.1);
plt.title('%d simulated datasets, with outliers' % N);

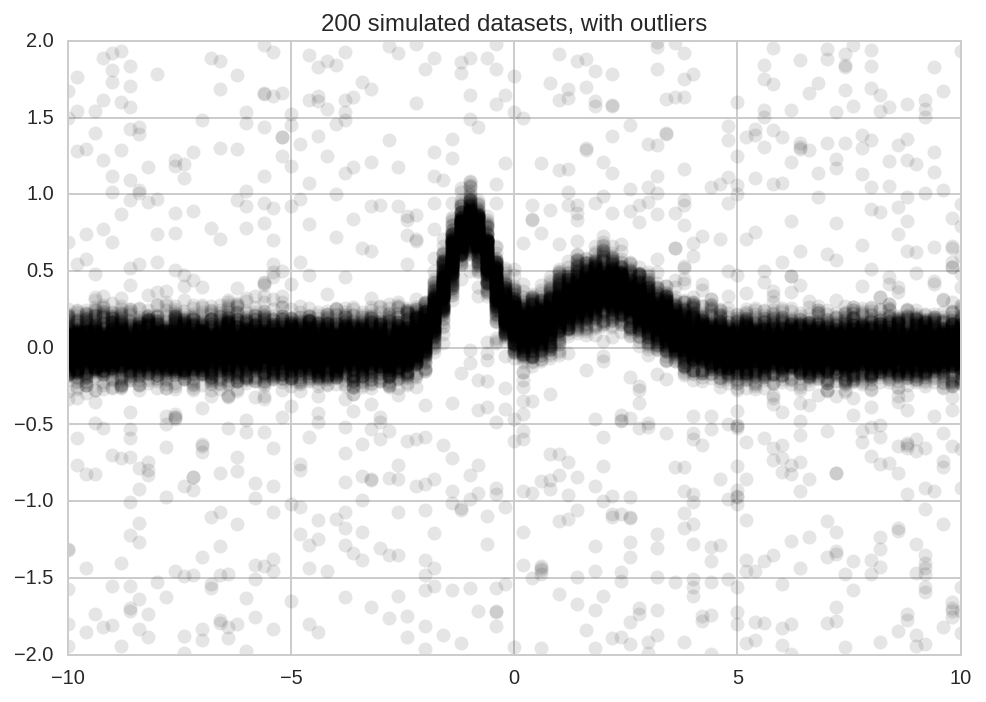
Model Fitting

curve_fit()

In [12]:

import scipy.optimize as so

In [13]:

from collections import namedtuple

In [14]:

# Model PDF to be maximized
def model_pdf(x, a1, a2, mu1, mu2, sig1, sig2):
    return (a1 * normpdf(x, mu1, sig1) +
            a2 * normpdf(x, mu2, sig2))

In [15]:

result = so.curve_fit(model_pdf, x, Y_data[0])

In [16]:

type(result), type(result[0]), type(result[1])

Out[16]:

(tuple, numpy.ndarray, numpy.ndarray)

In [17]:

result[0]

Out[17]:

array([ 1.04269146,  0.74819402, -1.01190597,  1.70754689,  0.5329466 ,
        0.78534337])

Using a namedtuple is a clean way to assign names to an array of paramenters:

In [18]:

Params = namedtuple('Params', 'a1 a2 mu1 mu2 sig1 sig2')

In [19]:

p = Params(*result[0])
p

Out[19]:

Params(a1=1.0426914570158334, a2=0.74819401768643379, mu1=-1.0119059745374694, mu2=1.7075468850195992, sig1=0.53294660190932697, sig2=0.78534337375473962)

Unfortunately, not much data is returned by curve_fit, a 2-element tuple with:

• array of best-fit parameters
• array of jacobian

Therefore curve_fit is not very useful for detailed comparison of fit results. A better interface for curve fitting would be lmfit.Model (see this other notebook).

In the current notebook we keep exploring further options offered by scipy.optimize.

least_squares()

As an example, we use the least_squares function which supports robust loss functions and constraints.

We need to define the residuals:

In [20]:

def residuals(p, x, y):
    return y - model_pdf(x, *p)

Then, we fit the N datasets with different loss functions storing result in a dict containing lists:

In [21]:

losses = ('linear', 'huber', 'cauchy')
Results = {}
for loss in losses:
    Results[loss] = [so.least_squares(residuals, (1,1,0,1,1,1), args=(x, y), loss=loss, f_scale=0.5)
                     for y in Y_data]

NOTE: For more details on robust fitting and on the different loss functions see Robust nonlinear regression in scipy.

In [22]:

# result = Results['cauchy'][0]
# for k in result.keys():
#     print(k, type(result[k]))

Tidying the results

Now we tidy the results, combining the results for the different loss functions in a single DataFrames.

We start with the glance function, which returns one row per fit result:

In [23]:

dg_tot = br.glance(Results, var_names=['loss', 'dataset'])
dg_tot.head()

Out[23]:

	success	cost	optimality	nfev	njev	message	dataset	loss
0	True	1.741101	0.000085	19	17	`ftol` termination condition is satisfied.	0	cauchy
1	True	1.425664	0.000023	12	11	`ftol` termination condition is satisfied.	1	cauchy
2	True	0.955012	0.000043	14	13	`ftol` termination condition is satisfied.	2	cauchy
3	True	1.637270	0.000007	13	13	`ftol` termination condition is satisfied.	3	cauchy
4	True	1.022261	0.000007	12	11	`ftol` termination condition is satisfied.	4	cauchy

In [24]:

dg_tot.success.all()

Out[24]:

True

Then we apply tidy, which returns one row per parameter.

Since the object OptimzeResult returned by scipy.optimize does only contains an array of parameters, we need to pass the names as as additional argument:

In [25]:

pnames = 'a1 a2 mu1 mu2 sig1 sig2'
dt_tot = br.tidy(Results, var_names=['loss', 'dataset'], param_names=pnames)
dt_tot.head()

Out[25]:

	name	value	grad	active_mask	dataset	loss
0	a1	1.013457	-4.760842e-09	0.0	0	cauchy
1	a2	0.848078	3.406909e-08	0.0	0	cauchy
2	mu1	-1.028959	8.220859e-06	0.0	0	cauchy
3	mu2	1.738017	-2.026311e-06	0.0	0	cauchy
4	sig1	0.515301	-8.535713e-05	0.0	0	cauchy

Finally, we cannot apply the augment function, since the OptimizeResult object does not include much per-data-point information (it may contain the array of residuals).

Plots

First we plot the peak position and sigmas distributions:

In [26]:

kws = dict(bins = np.arange(-2, 4, 0.1), histtype='step', lw=2)
for loss in losses:
    dt_tot.query('(name == "mu1" or name == "mu2") and loss == "%s"' % loss)['value'].hist(label=loss, **kws)
    kws['ax'] = plt.gca()
plt.title(' Distribution of peaks centers')
plt.legend();

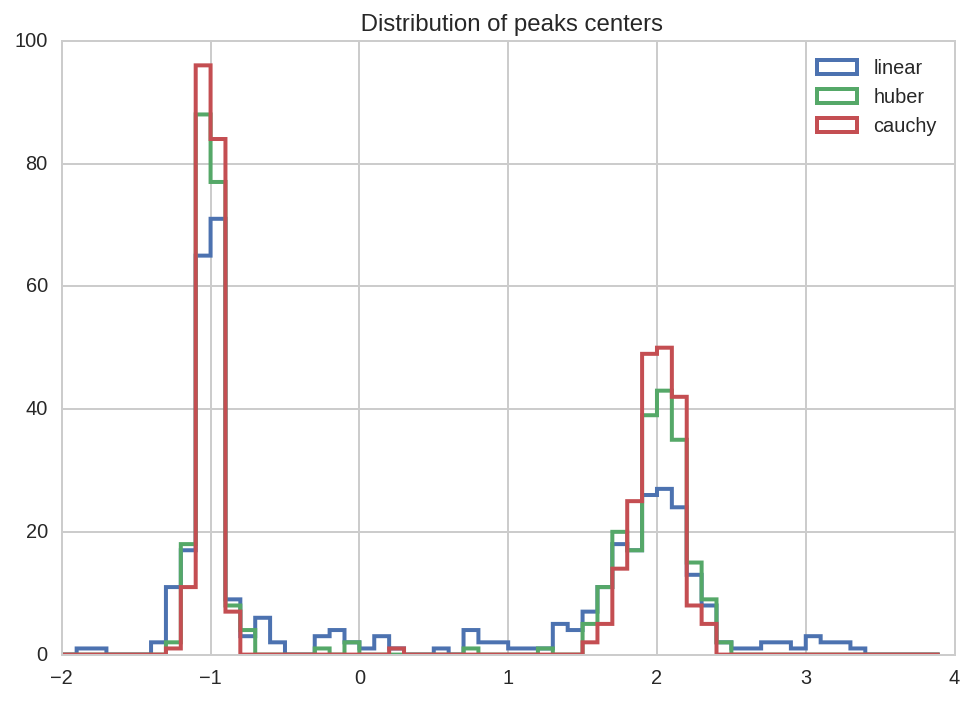
In [27]:

kws = dict(bins = np.arange(0, 4, 0.1), histtype='step', lw=2)
for loss in losses:
    dt_tot.query('(name == "sig1" or name == "sig2") and loss == "%s"' % loss)['value'].hist(label=loss, **kws)
    kws['ax'] = plt.gca()
plt.title(' Distribution of peaks sigmas')
plt.legend();

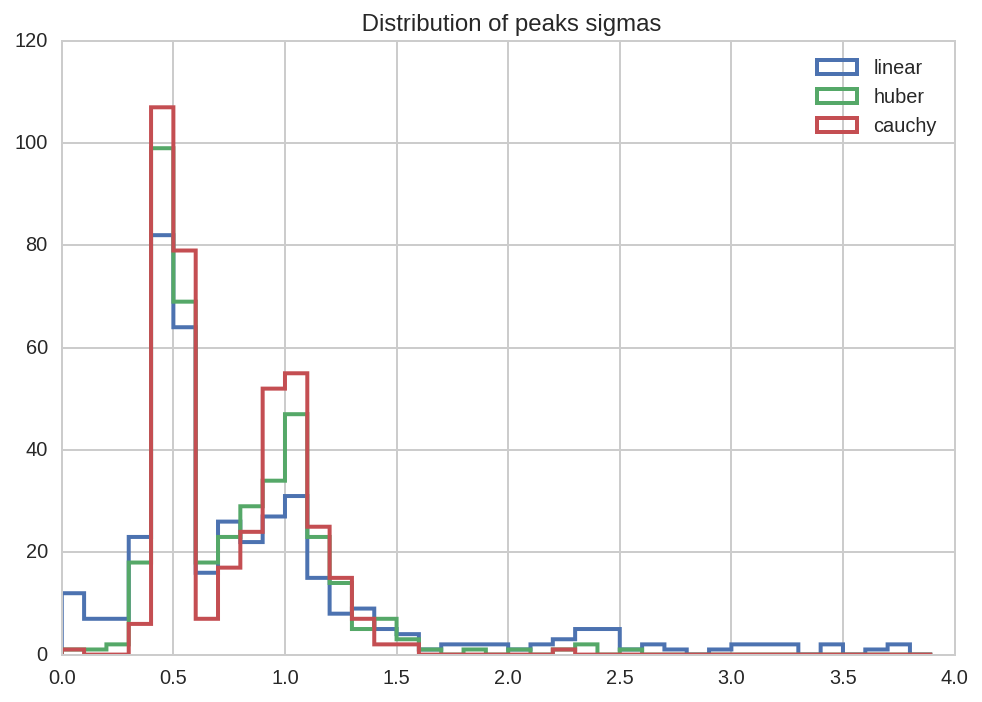
A more complete overview for all the fit paramenters can be obtained with a factorplot:

In [28]:

sns.factorplot(x='loss', y='value', data=dt_tot, col='name', hue='loss',
               col_wrap=4, kind='point', sharey=False);

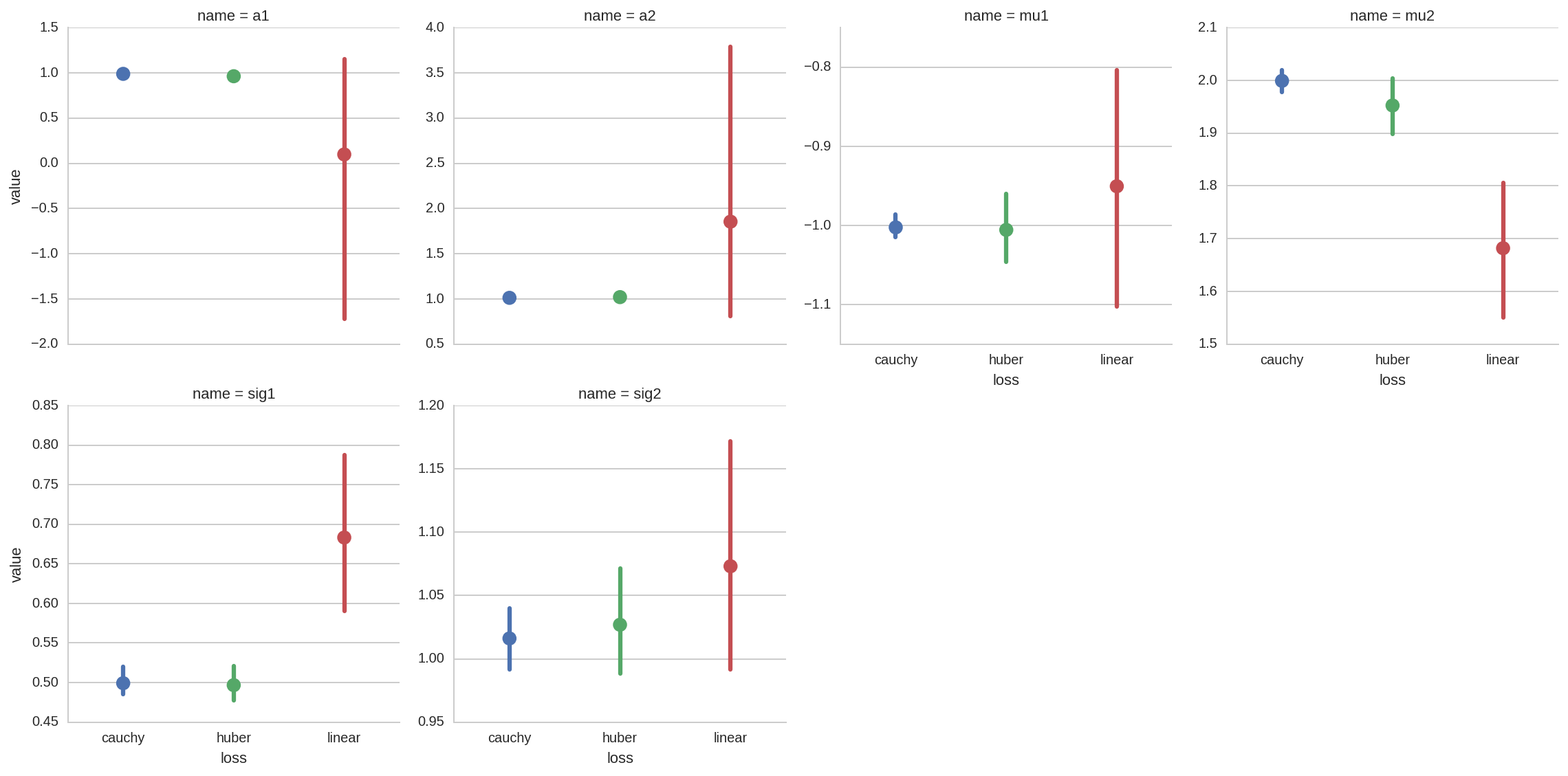
From all the previous plots we see that, as espected, using robust fitting with higher damping of outlier (i.e. cauchy vs huber or linear) results in more accurate fit results.

Finally, we can have a peek at the comparison of raw data and fitted models for a few datatsets.

Since OptimizeResults does not include “augmented” data we need to generate these data by evaluating the model with the best-fit parameters. We use seaborn’s FacetGrid, passing a custom function _plot for model evaluation:

In [29]:

def _plot(names, values, x, label=None, color=None):
    df = pd.concat([names, values], axis=1)
    kw_pars = br.tidy_to_dict(df)
    y = model_pdf(x, **kw_pars)
    plt.plot(x, y, lw=2, color=color, label=label)

In [30]:

grid = sns.FacetGrid(dt_tot.query('dataset < 9'), col='dataset', hue='loss', col_wrap=3)
grid.map(_plot, 'name', 'value', x=x)
grid.add_legend()
for i, ax in enumerate(grid.axes):
    ax.plot(x, Y_data[i], 'o', ms=3, color='k')
plt.ylim(-1, 1.5)

Out[30]:

(-1, 1.5)

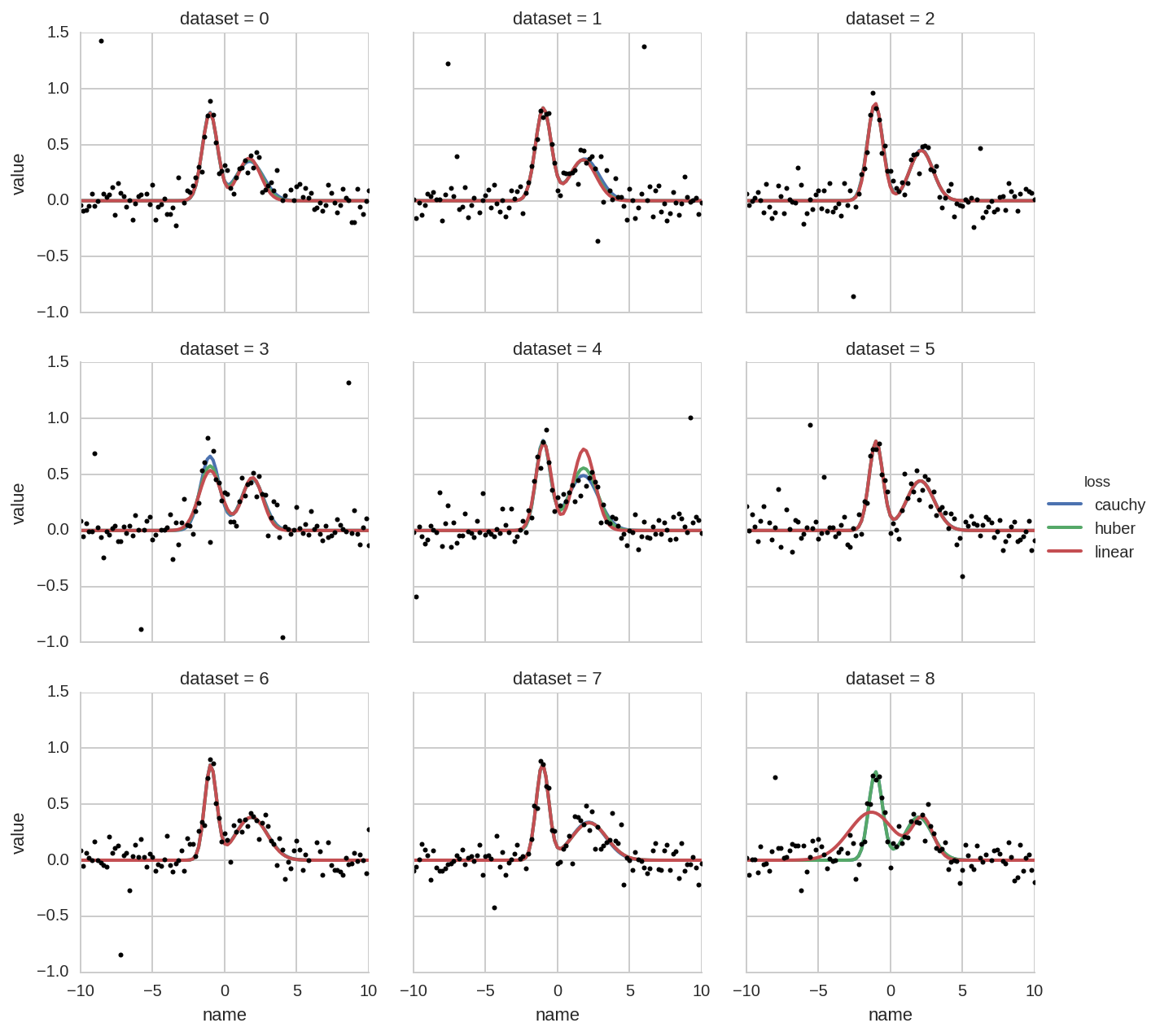
For comparison, the ModelResult object returned by lmfit, contains not only the evaluated model but also the evaluation of the single components (each single peak in this case). Therefore the above plot can be generated more straighforwardly using the “augmented” data. See the notebook pybroom-example-multi-datasets for an example.