PyBroom Example - Simple¶
This notebook is part of pybroom.
This notebook shows the simplest usage of pybroom when performing a curve fit of a single dataset. Possible applications are only hinted. For a more complex (and interesting!) example using multiple datasets see pybroom-example-multi-datasets.
In [1]:
import numpy as np
from numpy import sqrt, pi, exp, linspace
from lmfit import Model
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format='retina' # for hi-dpi displays
In [2]:
import lmfit
print('lmfit: %s' % lmfit.__version__)
lmfit: 0.9.5
In [3]:
import pybroom as br
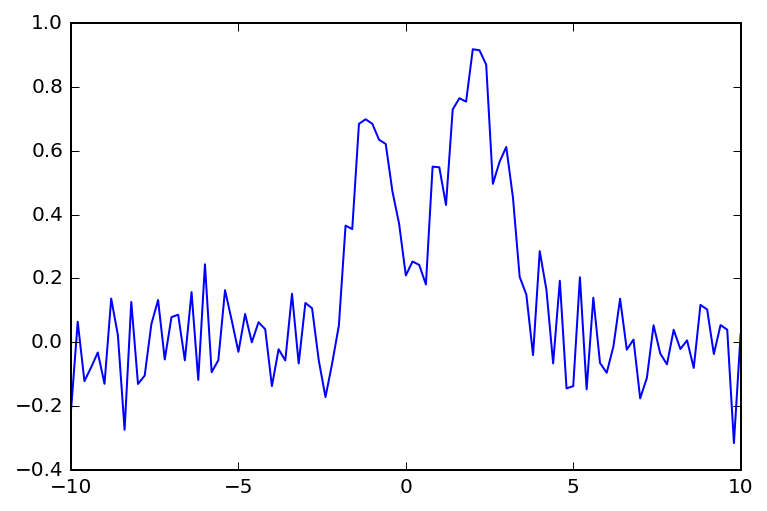
Create Noisy Data¶
In [4]:
x = np.linspace(-10, 10, 101)
In [5]:
peak1 = lmfit.models.GaussianModel(prefix='p1_')
peak2 = lmfit.models.GaussianModel(prefix='p2_')
model = peak1 + peak2
In [6]:
params = model.make_params(p1_amplitude=1, p2_amplitude=1,
p1_sigma=1, p2_sigma=1)
In [7]:
y_data = model.eval(x=x, p1_center=-1, p2_center=2, p1_sigma=0.5, p2_sigma=1, p1_amplitude=1, p2_amplitude=2)
y_data.shape
Out[7]:
(101,)
In [8]:
y_data += np.random.randn(*y_data.shape)/10
In [9]:
plt.plot(x, y_data)
Out[9]:
[<matplotlib.lines.Line2D at 0x7fa2c866ce48>]
Model Fitting¶
In [10]:
params = model.make_params(p1_center=0, p2_center=3,
p1_sigma=0.5, p2_sigma=1,
p1_amplitude=1, p2_amplitude=2)
result = model.fit(y_data, x=x, params=params)
Fit result from an lmfit Model can be inspected with with
fit_report or params.pretty_print():
In [11]:
print(result.fit_report())
[[Model]]
(Model(gaussian, prefix='p1_') + Model(gaussian, prefix='p2_'))
[[Fit Statistics]]
# function evals = 82
# data points = 101
# variables = 6
chi-square = 1.259
reduced chi-square = 0.013
Akaike info crit = -430.903
Bayesian info crit = -415.212
[[Variables]]
p1_center: -0.99098079 +/- 0.057195 (5.77%) (init= 0)
p1_amplitude: 1.01672511 +/- 0.094197 (9.26%) (init= 1)
p1_sigma: 0.54812438 +/- 0.058352 (10.65%) (init= 0.5)
p2_center: 1.99780286 +/- 0.064604 (3.23%) (init= 3)
p2_amplitude: 2.02456302 +/- 0.121975 (6.02%) (init= 2)
p2_sigma: 0.94915124 +/- 0.068652 (7.23%) (init= 1)
p1_fwhm: 1.29073427 +/- 0.137409 (10.65%) == '2.3548200*p1_sigma'
p1_height: 0.74000475 +/- 0.064033 (8.65%) == '0.3989423*p1_amplitude/max(1.e-15, p1_sigma)'
p2_fwhm: 2.23508032 +/- 0.161664 (7.23%) == '2.3548200*p2_sigma'
p2_height: 0.85095377 +/- 0.049431 (5.81%) == '0.3989423*p2_amplitude/max(1.e-15, p2_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(p1_amplitude, p1_sigma) = 0.630
C(p2_amplitude, p2_sigma) = 0.630
C(p1_amplitude, p2_sigma) = -0.321
C(p1_sigma, p2_sigma) = -0.299
C(p1_center, p2_sigma) = -0.261
C(p1_amplitude, p2_amplitude) = -0.246
C(p1_sigma, p2_amplitude) = -0.240
C(p1_center, p2_amplitude) = -0.199
C(p1_sigma, p2_center) = 0.196
C(p1_amplitude, p2_center) = 0.187
C(p1_center, p2_center) = 0.150
C(p1_center, p1_amplitude) = 0.105
C(p1_center, p1_sigma) = 0.102
C(p2_center, p2_sigma) = -0.101
In [12]:
result.params.pretty_print()
Name Value Min Max Stderr Vary Expr
p1_amplitude 1.017 -inf inf 0.0942 True None
p1_center -0.991 -inf inf 0.0572 True None
p1_fwhm 1.291 -inf inf 0.1374 False 2.3548200*p1_sigma
p1_height 0.74 -inf inf 0.06403 False 0.3989423*p1_amplitude/max(1.e-15, p1_sigma)
p1_sigma 0.5481 0 inf 0.05835 True None
p2_amplitude 2.025 -inf inf 0.122 True None
p2_center 1.998 -inf inf 0.0646 True None
p2_fwhm 2.235 -inf inf 0.1617 False 2.3548200*p2_sigma
p2_height 0.851 -inf inf 0.04943 False 0.3989423*p2_amplitude/max(1.e-15, p2_sigma)
p2_sigma 0.9492 0 inf 0.06865 True None
These methods a re convenient but extracting the data from the lmfit object requires some work and the knowledge of lmfit object structure.
pybroom comes to help, extracting data from fit results and returning pandas DataFrame in tidy format that can be much more easily manipulated, filtered and plotted.
Glance¶
Glancing at the fit results (dropping some verbose columns):
In [13]:
dg = br.glance(result)
dg.drop('model', 1).drop('message', 1)
Out[13]:
| method | num_params | num_data_points | chisqr | redchi | AIC | BIC | num_func_eval | success | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | leastsq | 6 | 101 | 1.258531 | 0.013248 | -430.902718 | -415.211995 | 82 | True |
The glance function returns a DataFrame with one row per fit-result object.
Application Idea¶
If you fit N models to the same dataset you can compare statistics such as reduced-\(\chi^2\)
Or, fitting several with several methods (and datasets) you can study the convergence properties using reduced-\(\chi^2\), number of function evaluation and success rate.
Tidy¶
Tidy fit results for all the parameters:
In [14]:
dt = br.tidy(result)
dt
Out[14]:
| name | value | min | max | vary | expr | stderr | init_value | |
|---|---|---|---|---|---|---|---|---|
| 0 | p1_amplitude | 1.016725 | -inf | inf | True | None | 0.094197 | 1.0 |
| 1 | p1_center | -0.990981 | -inf | inf | True | None | 0.057196 | 0.0 |
| 2 | p1_fwhm | 1.290734 | -inf | inf | False | 2.3548200*p1_sigma | 0.137410 | NaN |
| 3 | p1_height | 0.740005 | -inf | inf | False | 0.3989423*p1_amplitude/max(1.e-15, p1_sigma) | 0.064033 | NaN |
| 4 | p1_sigma | 0.548124 | 0.000000 | inf | True | None | 0.058353 | 0.5 |
| 5 | p2_amplitude | 2.024563 | -inf | inf | True | None | 0.121975 | 2.0 |
| 6 | p2_center | 1.997803 | -inf | inf | True | None | 0.064604 | 3.0 |
| 7 | p2_fwhm | 2.235080 | -inf | inf | False | 2.3548200*p2_sigma | 0.161665 | NaN |
| 8 | p2_height | 0.850954 | -inf | inf | False | 0.3989423*p2_amplitude/max(1.e-15, p2_sigma) | 0.049431 | NaN |
| 9 | p2_sigma | 0.949151 | 0.000000 | inf | True | None | 0.068653 | 1.0 |
The tidy function returns one row for each parameter.
In [15]:
dt.loc[dt.name == 'p1_center']
Out[15]:
| name | value | min | max | vary | expr | stderr | init_value | |
|---|---|---|---|---|---|---|---|---|
| 1 | p1_center | -0.990981 | -inf | inf | True | None | 0.057196 | 0.0 |
Augment¶
Tidy dataframe with data function of the independent variable (‘x’). Columns include the data being fitted, best fit, best fit components, residuals, etc.
In [16]:
da = br.augment(result)
da.head()
Out[16]:
| x | data | best_fit | residual | Model(gaussian, prefix='p1_') | Model(gaussian, prefix='p2_') | |
|---|---|---|---|---|---|---|
| 0 | -10.0 | -0.213844 | 1.711221e-35 | 0.213844 | 1.614414e-59 | 1.711221e-35 |
| 1 | -9.8 | 0.063797 | 2.401207e-34 | -0.063797 | 6.076585e-57 | 2.401207e-34 |
| 2 | -9.6 | -0.122706 | 3.223075e-33 | 0.122706 | 2.002088e-54 | 3.223075e-33 |
| 3 | -9.4 | -0.079427 | 4.138359e-32 | 0.079427 | 5.774119e-52 | 4.138359e-32 |
| 4 | -9.2 | -0.032691 | 5.082799e-31 | 0.032691 | 1.457697e-49 | 5.082799e-31 |
The `augment <>`__ function returns one row for each data point.
In [17]:
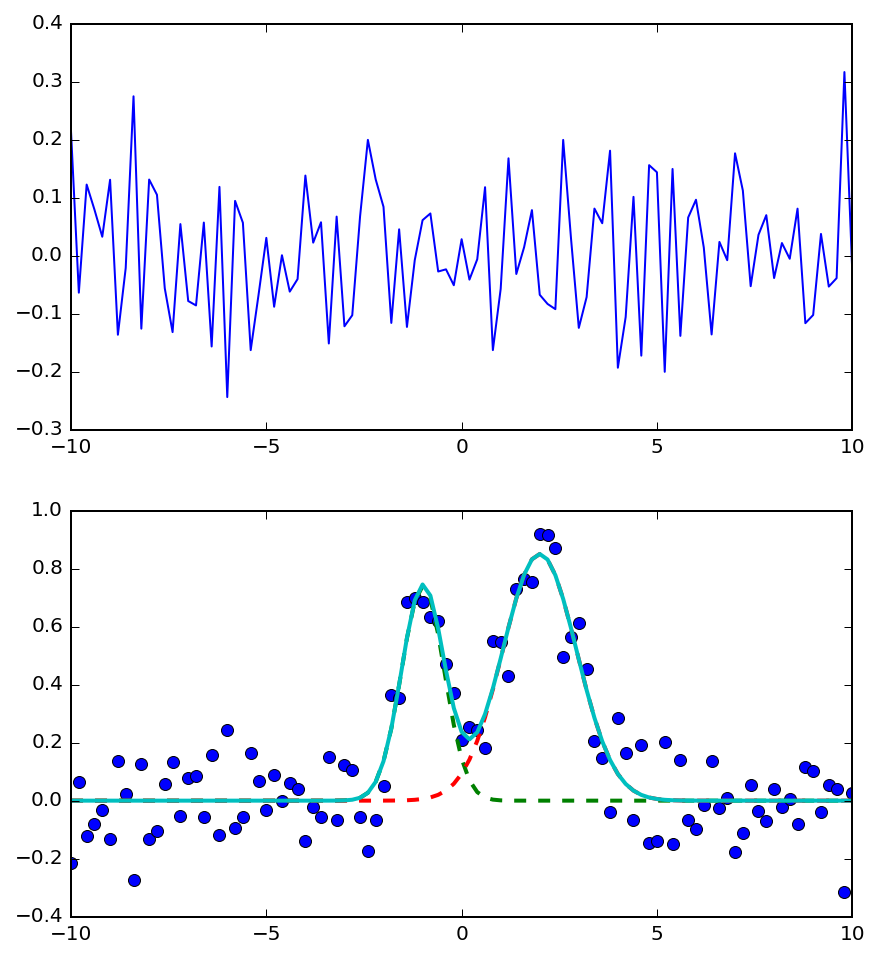
d = br.augment(result)
In [18]:
fig, ax = plt.subplots(2, 1, figsize=(7, 8))
ax[1].plot('x', 'data', data=d, marker='o', ls='None')
ax[1].plot('x', "Model(gaussian, prefix='p1_')", data=d, lw=2, ls='--')
ax[1].plot('x', "Model(gaussian, prefix='p2_')", data=d, lw=2, ls='--')
ax[1].plot('x', 'best_fit', data=d, lw=2)
ax[0].plot('x', 'residual', data=d);
Application Idea¶
Fitting N datasets with the same model (or N models with the same
dataset) you can automatically build a panel plot with seaborn using
the dataset (or the model) as categorical variable. This example is
illustrated in
pybroom-example-multi-datasets.